FLECHAS

La generalización de las mónadas
“Las flechas hacen explícita la dependencia del input” (John Hughes )

“Cuando definimos el interfaz a un componente software, queremos que revele lo menos posible de su implementación” (John Hughes)

---

El concepto de flecha

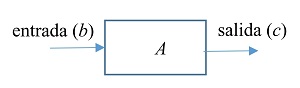
Una flecha (arrow en inglés) A b c es una estructura abstracta que representa una computación A de entrada de tipo b y que devuelve de salida un tipo c.


Las flechas guardan una relación con las funciones, pero no son funciones. Son categorías de funciones: las funciones de entrada b y salida c. Las flechas no explican ni detallan el cómo se obtiene c a partir de b. Las flechas son de tipo declarativo.

El concepto de flecha es más general que el de morfismo (también denominado “flecha”) de la teoría de categorías. Un morfismo es una relación entre un objeto A hacia otro objeto B de una categoría y que se representa como A→B.

Las flechas suministran una disciplina para estructurar programas. Utilizan la analogía del circuito. El lenguaje de las flechas parece un lenguaje de definición de hardware. Los programas parecen estáticos y no se ve cómo se procesan los datos.

Hay diferentes tipos de flechas: divisores (splitters), conmutadores (switches), retardadores (delays), integradores, conversores de funciones en flechas (liftings), etc.


Flechas vs. Mónadas

• El concepto de flecha es una generalización del concepto de mónada. Al ser más genéricas que las mónadas, resuelven un rango de problemas más amplio.
  
  Una flecha está definida con dos tipos (b y c). En cambio, la mónada solo tiene uno, a. El tipo monádico M a representa una computación M que devuelve a. La flecha A b c representa una computación A de entrada de tipo b y que devuelve de salida un tipo c.
  
  En las flechas se hace explícita la dependencia de las entradas. No así en las mónadas. La lógica de un programa con flechas se hace más explícita que con mónadas.
  
  
• Las mónadas y las funciones son casos particulares de flechas. Las flechas tienen entrada y salida, como las funciones, pero las flechas puede tener múltiples entradas. En las mónadas hay una entrada o una salida o ambas (entrada y salida), dependiendo de la interpretación.
  
  
• Las flechas generalizan la composición de funciones que realizan las mónadas. En un lenguaje funcional sin mónadas ni flechas, la composición de funciones está limitada a que una función tenga como entrada el resultado de la función precedente.
  
  
• Las flechas permiten computación paralela gracias a las múltiples entradas. Las mónadas solo admiten computación secuencial.
  
  
• Las flechas permiten que las computaciones sean parcialmente estáticas (independientes del input). Ni las funciones ni las mónadas pueden manejar información estática; solo manejan información dinámica.
  
  
• Mónadas y flechas permiten implementar computaciones de efectos colaterales de tipo imperativo. Pero las flechas son más flexibles que las mónadas, por lo que admiten más formas combinatorias que las mónadas. Esto permite a los programadores organizar una mayor variedad de efectos colaterales que con las mónadas.
  
  
• Las flechas pueden enrutar datos a otras flechas en tiempo de ejecución. Tienen encadenamiento dinámico en función de los datos. Las mónadas tienen encadenamiento estático.
  
  
• Las combinaciones entre flechas producen nuevas flechas. En cambio, las mónadas se combinan con funciones.
  
  
• Las flechas son más expresivas que las mónadas, más intuitivas y más fáciles de entender. Por lo tanto, los programas con flechas son más fáciles de depurar que los de mónadas.
  
  
• Las flechas son más fáciles de implementar que las mónadas, aunque las flechas requieren mayor esfuerzo de diseño que las mónadas, pues las flechas deben satisfacer una serie de leyes (las leyes de las flechas).
  
  
• Los compiladores se optimizan mejor con flechas que con mónadas.
  
  
• Con flechas se favorece la reutilización de código más que con mónadas.

Operaciones con flechas

1. arr. Es el constructor principal. Convierte una función en una flecha.
   Si tenemos una función de tipo b → c, podemos construir la flecha de tipo A b c (podemos leerlo como la flecha A de origen b y extremo c).
   
   
   Definición: arr :: (b → c) → A b c
   
   
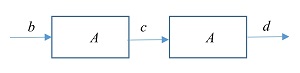
2. >>>. Es el operador de composición de flechas. Es equivalente a “>>=” (bind) de las mónadas. Pone dos flechas en secuencia, conectando la salida de la primera flecha con la entrada de la segunda.
   
   
   
   Definición: >>> :: A b c → A c d → A b d
   
   Si la primera flecha es de tipo A b c, la segunda flecha debe ser de tipo A c d. La flecha resultante es de tipo A b d.
   
   
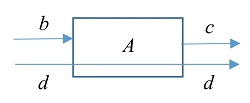
3. first. Generaliza una flecha (dinámica) A b c en otra flecha con una parte estática d (presente en la entrada y en la salida) como segundo componente de entrada y de salida.
   
   
   
   Definición: first :: A b c → A (b d) (c d)
   
   
4. second. Es la operación dual de first. Generaliza una flecha (dinámica) A b c en otra flecha con una parte estática d (presente en la entrada y en la salida) como primer componente de entrada y de salida.
   
   
   
   Definición: second :: A b c → A (d b) (d c)
   
   
5. ***. Fusiona dos flechas en una, con dos tipos de componentes.
   
   
   Definición: *** :: A b c → A u v → A (b u) (c v)
   
   
6. &&&. Combina dos flechas que tienen la misma entrada en una flecha con las dos salidas.
   
   
   Definición: &&& :: A b c → A b d → A b (c d)

Realmente solo existen tres combinaciones primitivas, que son las tres primeras. Las otras tres son combinaciones derivadas. Por ejemplo, *** es la combinación de first y second.


Ejemplo

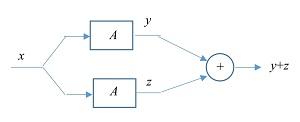
Tenemos el gráfico siguiente:


A x y (flecha de entrada x y salida y)
A x z (flecha de entrada x y salida z)
y+z (suma de de las salidas de ambas flechas)


Transformadores de flecha (arrow transformers)

Un transformador de flecha es un tipo de flecha parametrizada sobre otro tipo de flecha, de tal manera que flechas del segundo tipo se pueden hacer corresponder con flechas del primero. De hecho, esto se corresponde con el concepto de funtor de la teoría de categorías. Con este mecanismo es posible construir una variedad infinita de flechas.


Implementación en MENTAL
En MENTAL, podemos hacer las siguientes consideraciones:

• El símbolo de la flecha horizontal está reservado para la primitiva “Condición”. Pero podemos definir una flecha de la manera siguiente:
  
  Por ejemplo, la flecha A como la clase de funciones que tienen de entrada a y de salida b es:
  
  
  ⟨( A(a b) = {⟨( A ←( A(a) = b) )⟩ )⟩
  
  
• Las expresiones descriptivas se pueden especificar de muchas formas. Por ejemplo:
  
  
  • Mediante expresiones genéricas parametrizadas. Como en el caso de las mónadas, en las flechas está implícita una generalización.
    
    
  • Mediante sustituciones diferidas (representaciones).
    
    
  • Mediante la especificación de solo valores de entrada y salida de funciones.
    
    
  • Mediante calificadores.
  
  
• MENTAL es muy adecuado para la programación funcional reactiva porque todo sistema está integrado en un entorno y forma parte de él. Es muy fácil especificar las interacciones con el entorno mediante expresiones genéricas (parametrizadas o no), con cambios a nivel interno del sistema o a nivel externo.
  
  
• MENTAL no introduce leyes como en las flechas, sino grados de libertad. Las leyes de MENTAL son relaciones entre las primitivas.
  
  
• Las primitivas de MENTAL son los combinadores universales.
  
  
• Las mónadas y las flechas se inventaron como abstracciones complementarias para los lenguajes de programación funcionales. MENTAL es un paradigma universal basado en primitivas que representan grados de libertad y que representan la abstracción suprema, por lo que a partir de estas primitivas es posible definir otras abstracciones de menor nivel. Los problemas se resuelven mejor cuanto mayor es el nivel de abstracción.
  
  
• Cuando se dispone de un lenguaje universal y un paradigma universal, no tiene sentido crear lenguajes de paradigmas particulares, a menos que se deriven de lo universal. Paradójicamente, un lenguaje universal es más simple que un lenguaje particular. Con un lenguaje universal (reflejo de un paradigma universal) se disuelven los egos de los diferentes lenguajes y paradigmas particulares.

---

Adenda
Orígen de las flechas

El concepto de flecha fue introducido por John Hughes [2000, 2005], como generalización del concepto de mónada para el lenguaje funcional Haskell, motivado por la búsqueda de un analizador sintáctico (parser) eficiente, como una alternativa a los basados en mónadas, que eran poco eficientes y consumían mucha memoria.

Hughes se inspiró particularmente en el analizador sintáctico diseñado por Swierstra y Duponcheel [1996], que constaba de dos componentes secuenciales: uno rápido (estático), que evalúaba de forma general si la entrada merecía ser analizada, y otro lento (dinámico) que realizaba el trabajo de detalle. La notación que utilizó Hughes fue point-free.

Ross Patterson [2001] introdujo una nueva notación más fácil de usar con la que algunas leyes se podían expresar directamente. Pero esta nueva notación resultó ser insuficiente para el tratamiento general de las flechas.

Aunque el artículo de Hughes apareció en el 2000, con los parsers estilo flecha, una implementación práctica no estuvo disponible hasta Mayo de 2005: PArrows, desarrollado por Einar Karttunen.

Desde que Hughes publicó su primera definición en 2000, las leyes y las operaciones se han redefinido varias veces. Recientes formalizaciones [Lindley y otros, 2010] requieren solo 5 leyes.


Aplicaciones de las flechas

Las flechas se están aplicando en: analizadores sintácticos (parsers), diseño de circuitos, y metaprogramación (programas que generan programas). Y también en dos campos especiales:

• Programación funcional reactiva. Es un tipo de programación en el que las entradas al sistema no se conocen a priori. El sistema interacciona con el entorno mediante entradas y salidas, devolviendo un valor como respuesta del sistema tras un tiempo predeterminado, y continuando con su ciclo de ejecución. Este paradigma de programación se utiliza para animación por ordenador, robótica móvil, robótica humanoide, sistemas de tiempo real, proceso paralelo e interfaces gráficas de usuario.
  
  
• Programación point-free. El estilo de programación libre de puntos, también denominado “programación tácita” consiste en que las funciones no tienen prefijados o identificados los argumentos (los “puntos”). Las expresiones se forman componiendo funciones, entre las cuales están los combinadores que manipulan los argumentos. El estilo point-free es conveniente para establecer propiedades generales, pero incómodos para las definiciones específicas. Las flechas proporcionan una sintaxis más natural para este tipo de programación.

Bibliografía

• Asada, Kazuyuki. Arrows are strong Monads. Internet, 2010.
  
  
• Flechas en Haskell y otros artículos sobre flechas. http://www.haskell.org/arrows.
  
  
• Hughes, John. Generalizing Monads to Arrows. In Science of Computer Programming, 37: 67-111, May 2000. Disponible online. (El artículo clave sobre flechas. Explica también el concepto de mónada).
  
  
• Hughes, John. Programming with Arrows. In 5th International Summer School on Advanced Functional Programming, LNCS 3622, pp 73-129, Springer, 2005. Disponible online. (Una introducción a las flechas y su notación).
  
  
• Jacobs, Bart; Heunen, Chris; Hasuo, Ichiro. Categorical Semantics for Arrows. Journal of Functional Programming 19 (3-4): 403–438, 2009.
  
  
• Lindley, Sam; Wadler, Philip; Yallop, Jeremy. The Arrow Calculus. Journal of Functional Programming 20 (1): 51–69, January 2010. Disponible online.
  
  
• Lindley, Sam; Wadler, Philip; Yallop, Jeremy. Idioms are oblivious, arrows are meticulous, monadas are promiscuos. Internet, 2008.
  
  
• McBride, Conor; Paterson, Ross. Applicative programming with effects. Journal of Functional Programming, 18 (1): 1-13, 2008.
  
  
• Moggi, Eugenio. Notions of computations and monads. Information and Computation, 93 (1): 55-92, 1991.
  
  
• Paterson, Ross. A New Notation for Arrows. In ICFP, Firence, Italy, pp. 229-240, Sep. 2001. Disponible online. (Una nueva notación para las flechas, que está disponible en el compilador Haskell de Glasgow).
  
  
• Paterson, Ross. Arrows and Computation. In The Fun of Programming, pp. 201-222, Palgrave, 2003. (Presentación general sobre flechas).
  
  
• Swierstra, S.D.; Duponcheel, Luc. Deterministic, error-correcting combinator parsers. In Advanced Functional Programming, 1129 of LNCS-Tutorial, pp. 184-207. Springer-Verlag, 1996.